Existen todavía algunas familias de grafos que se derivan
del concepto de grafos conexos. Este es el caso de los grafos eulerianos y
los grafos hamiltonianos. Estas familias de grafos nos permiten resolver
el famoso problema de los puentes de Königsberg:
¿cuándo es posible hacer un recorrido de una figura (en este caso de un grafo
múltiple) sin pasar dos veces por la misma línea o por el mismo vértice?
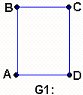
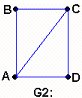
Tenemos dos grafos G1 y G2; es posible recorrer uno de
ellos sin repetir ninguna línea, pero el otro no. ¿Cuál es cuál? Es evidente
que el grafo G1 no puede ser recorrido sin repetir alguna de sus líneas,
mientras que el grafo G2 sí.


Grafos Eulerianos
Recorrido cerrado
Cubre todas las líneas de un grafo, comenzando y terminando en un mismo
vértice, recorriendo sin repetición y en forma continua todas las líneas de un
grafo G cualquiera. Cuando tal recorrido existe, se denomina eulerianoy un
grafo que se puede trazar mediante un recorrido euleriano se llamagrafo
euleriano. En la fig. 3.11, G1 es obviamente un grafo euleriano; G2 no lo
es, a pesar de que se puede trazar continuamente, ya que el recorrido comienza
y termina en vértices distintos; finalmente, G3 no es un grafo euleriano,
porque no se puede trazar continuamente.

Diremos que un grafo G es la unión disjunta de ciclos,
si podemos descomponer a G como la unión de ciclos que no tienen líneas en
común, aunque se permite que tengan, al menos, un vértice en común.

En la figura el grafo se puede descomponer como la unión
disjunta de los ciclos C = v1v2v3v4v5v6v1; C' = v1v7v5v1; C'' = v2v7v4v2; C'''
= v3v8v9v3 y el recorrido euleriano para el grafo G viene dado por la
secuencia de sus líneas 1, 2,..., 15.
OBSERVACION : Esta descomposición por lo general no es única. El
grafo de la fig. 3.11 admite otra descomposición como unión disjunta de ciclos,
por ejemplo, C = v1v2v7v1; C' = v3v4v2v3; C'' = v3v8v9v3; C''' = v7v4v5v7;
C'''' = v5v1v6v5 .
Recíprocamente, supongamos que G es una unión disjunta de ciclos. Sea C un
ciclo cualquiera en G. Si entonces G es un ciclo y por lo tanto euleriano. Si existe un ciclo C' en G que tiene un vértice v en común con
C (por hipótesis). Si G es la unión de C y C', entonces, comenzando en v
trazamos C y luego C', obteniendo así un recorrido euleriano de G. Si la unión
de C y C' no es todo G, existe un ciclo C'' que tiene algún vértice v' en común
con C o con C', digamos por ejemplo con C'. Si G es la unión de C, C' y C'',
entonces comenzando en v trazamos C, luego trazamos C' hasta llegar a v' y
luego trazamos C'' hasta completar C', luego regresamos a v como ilustra el
diagrama de la fig. 3.13.
Así, obtenemos un recorrido euleriano de G. Si la unión de C, C' y C'' no es
todo G, continuamos con este procedimiento hasta obtener un recorrido euleriano
de G.
COROLARIO 2: Un grafo conexo es euleriano si y sólo si
todos sus vértices tienen valencia par. (Este teorema rige también para
multigrafos).
Demostración:
En un recorrido euleriano, cuando visitamos un vértice, necesitamos al menos
dos líneas distintas adyacentes al vértice (una para llegar al vértice y otra
para salir de él), incluyendo al vértice inicial, porque tenemos que regresar a
él para concluir el recorrido. Esto significa, que cada vértice contribuye con
un número par de líneas y, por lo tanto, su valencia es par.
Grafos Hamiltonianos
Definición: Un circuito o ciclo hamiltoniano es un ciclo simple que contiene todos
los vértices de G.
Un circuito hamiltoniano es una trayectoria que empieza y termina en el mismo
vértice y pasa por cada vértice una sola vez.
Ejemplos:
¿Cuál de los grafos siguientes admite un circuito hamiltoniano?
Solución
(a) No admite circuitos hamiltonianos. El razonamiento es el siguiente: Si se
empieza en v1, v2, v3, v4 y si se está en los demás vértices, en el v5 se estará dos
veces.
Si se empieza en v5, para luego ir a los vértices v1 o v4 ó a v3 o v2 respectivamente, se
tendrá que pasar de nuevo por v5 (puesto que se empezará en v5). Para completar el
circuito, se debe regresar a v5, por lo que se pasa tres veces por él.
(b) Un ciclo hamiltoniano es: v1 e1 v2 e2 v3 e3 v4 e4 v1
Teorema. Sea G un grafo conexo con n vértices, donde n≥3.
Si la suma de los
grados de cada par de vértices no adyacentes es mayor o igual a n, entonces G tiene
un circuito hamiltoniano.

No hay comentarios:
Publicar un comentario